A Unified Influence Maximization Processing Framework for Independent Cascade Model and Its Extensions
Table of Contents
Abstract
The word-of-mouth effect on social networks – opinion propagation – nowadays plays an important role in marketing. The influence maximization problem aims at maximizing the word-of-mouth effect and formulates such goal as a combinatorial optimization problem. As an important process of the influence maximization problem, evaluating influence is \#P-hard which cannot be affordable in a polynomial time. Accordingly, devising fast influence evaluation/approximation algorithm is crucial. We propose a scalable influence approximation algorithm called IPA. The main idea of IPA is considering an independent influence path as an influence evaluation unit. Using that idea, IPA approximates influence an order of magnitude faster and more accurately, and uses less much less memory than PMIA, the current state of the art approximation algorithm. In addition, IPA is applicable to independent cascading (IC) model and its extensions (IC-N, t-IC, t-IC-N models), whereas PMIA is only adaptable to IC and IC-N models. We implement and demonstrate a desktop application which finds the most influential nodes and visualizes influence paths. The application is accessible at http://dm.postech.ac.kr/ipa_demo.
Paper
Desktop Application
We provide a windows desktop application which finds the seed nodes and visualizes the influence paths using IPA algorithm. IPA algorithm is implemented by C++. The user interface uses QT4 framework, and the graph visualization uses Graphviz library.
Prerequisite – IMPORTANT
To run our application, Graphviz library should be installed. The windows libarary is available at http://www.graphviz.org/pub/graphviz/stable/windows/graphviz-2.28.0.msi.
Data
Format
The first line of a graph data file consists of two integers; the first one is the number of nodes and the second one is the number of edges.
The second to last line also consist of two integers which represent node-id. node-id should range over from \(0\) to \(\text{<number of nodes>} - 1\). When the graph is directed, an edge starts from the first node-id to the second id. Otherwise, the order of two integers is not important.

The following is an example of a data file that represent the above graph.
6 5 # <# of nodes> <# of edges> 0 1 # edge description 1 2 2 3 3 1 4 5
Available Datasets
Here we refer to two publicly available dataset repositories.
- Wei Chen's project page
The data format used here complies with our data file format specification. After downloading them, you can apply them to our application without any modification.
- Stanford Large Network Dataset Collection
- Epinion
- Stanford
- Patent
- LiveJournal
- and more …
The data format used here does not follow our data file format specification. Thus, we provide a windows data preprocessor binary in Download Application Binary. The usage is that after (1) putting the preprocessor in dataset location and (2) moving into the dataset location in window command line, execute the following command.
path-to-preprocessor> IPA_preprocessor.exe <datafile>
After executing, in dataset location, the preprocessed datafile named
preprocessed_<datafile>and id-matching table from original dataset to preprocessed datasetmatching_table_<datafile>are generated.
Download Application Binary
If you have any trouble in downloading or excuting the file, please e-mail us.
Usage
After you download and extract the .zip file, execute the binary named IPA_Demo.exe and set a graph file and parameters as follows.
Network Setting
- Network
path: the path of network dataset filedirected: when checked, the network is directed, otherwise, undirected
- Weighting Model
- One of
ICandWCIC: an uniform probability is assigned to all edgesWC: for a node \(v\) and \(v\)'s in-neighbor set \(N_{in}(v)\), \(\frac{1}{|N_{in}(v)|}\) is assigned to each edge \(u \in N_{in}(v)\)
PP: the uniform propagation probability whenICis checked
- One of
Parameter Setting
- Diffusion Model
- One of
IC,t-IC,IC-N, andt-IC-N
- One of
- General Parameter
k: the number of seed nodesThreshold: the lower bound of the probability that an influence path can haveMultiplier: the number of entries in priority queue (Multiplier \(\times\) k)
- t- options
T: the ending stage of influence diffusionalpha: decaying speed of \(\delta(\cdot)\), the larger value means the higher decaying speed
- -N option
quality factor: the probability that a positive opinion is kept when a node is activated
An Examplary Scenario
This scenario is tested on Windows 7 Professional 32bit and 64bit.
Here we provide an examplary scenario of using our IPA application.
The root directory of this scenario is C:/IPA Demo.
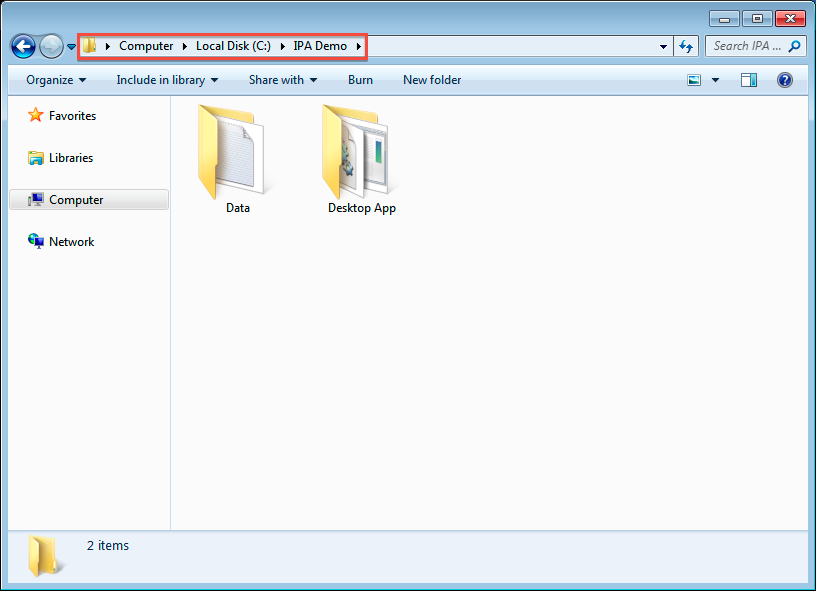
Download and Extract
- download the desktop application binary(ipa-desktop.zip) and data converter(ipa-preprocessor.zip – it's optional) from Download Application Binary
- download datafile (e.g. NetHEPT and NetPHY) from Available Datasets
- extract ipa-desktop.zip into
C:/IPA Demo/Desktop App
- extract graphdata.zip from Wei Chen's project page
- extract ipa-preprocessor.zip into
C:/IPA Demo/Data(optional to handle dataset from Stanford Large Network Dataset Collection)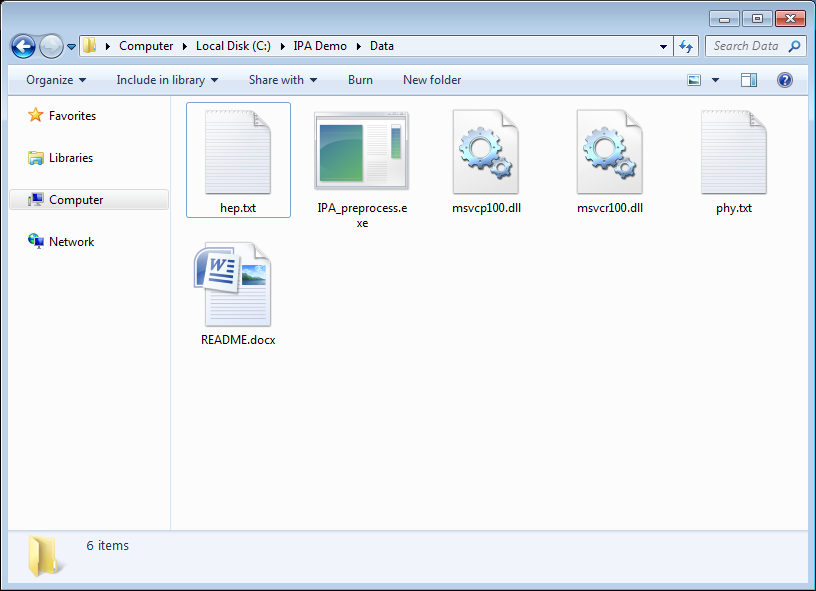
Run IPA algorithm
- move to
C:/IPA Demo/Desktop APP - execute
IPA_Demo.exe - set dataset
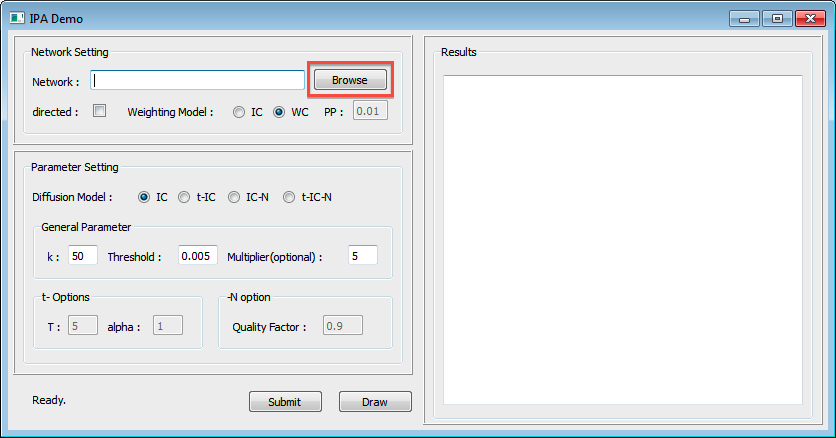
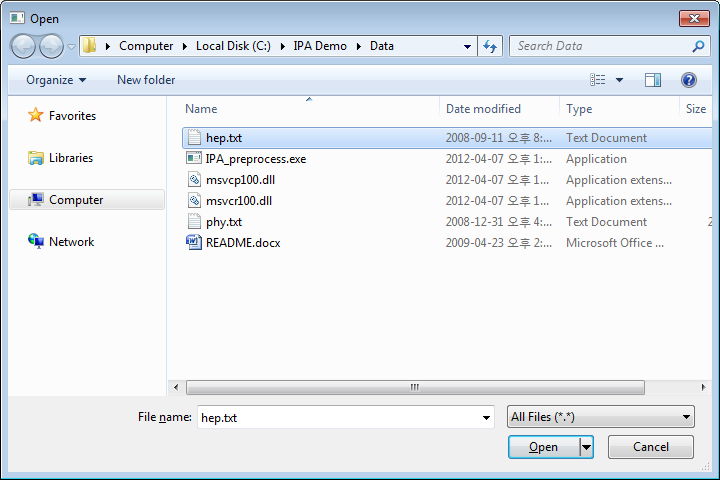
- set parameters and push
submitbutton- default value is enough to see result
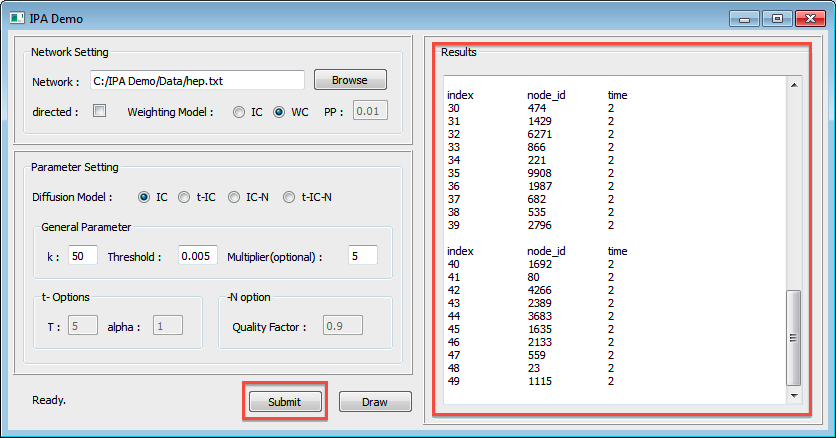
Visualize
After getting seed nodes from IPA algorithm,
- push
drawbutton, a new pop-up window appears
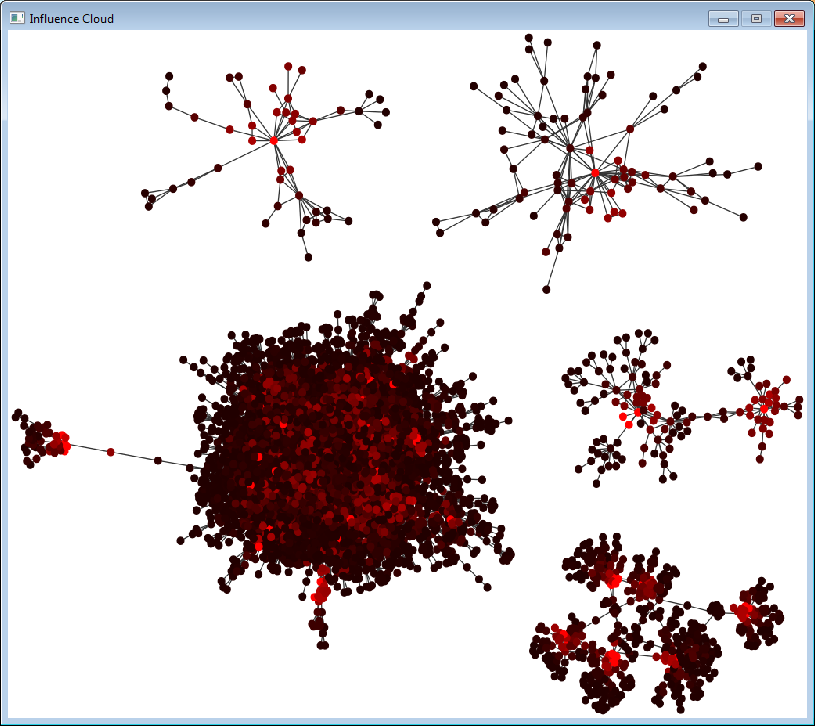
- to draw again, you should run IPA again – push
submitbutton again